Kto otrzyma "matematycznego Nobla"?

Już 22 sierpnia w Madrycie rozpoczyna się kolejny Międzynarodowy Kongres Matematyków, który zgromadzi ponad 5000 matematyków z całego świata. Zostanie na nim wręczony medal Fieldsa, najważniejsze i najbardziej prestiżowe wyróżnienie w matematycznym światku. Wiele wskazuje, że powędruje on do Rosjanina Grigorija Perelmana, tym samym potwierdzając oficjalnie, że zaprezentowany przez niego kilka lat temu dowód tzw. hipotezy Poincarégo jest prawidłowy.

W 1904 roku Henri Poincaré zadał prosto brzmiące pytanie: czy każda trójwymiarowa zwarta i jednospójna rozmaitość jest homeomorficzna z 3-sferą? Hipoteza mówi, że tak, ale udowodnić tego nikt nie potrafił.

Wiemy, że jeśli owieniemy wokół jabłka elastyczną pętlę, przesuwając ją (ale nie zdejmując!) będziemy mogli w końcu doprowadzić do sytuacji, że skurczy się ona do małych rozmiarów - teoretycznie, nawet do punktu. Są jednak obiekty, które zachowują się inaczej, na przykład obwarzanki. Jeśli owiniemy wokół obwarzanka pętlę w odpowiedni sposób, nie będziemy mogli zmniejszać dowolnie jej długości. Istnieje więc fundamentalna różnica pomiędzy dwuwymiarowymi sferami (jabłkami), a torusami (obwarzankami). Co więcej, tylko sfery - oraz "podobne" (tzn. homeomorficzne) do nich obiekty są jednospójne, czyli pozwalają na zredukowanie naszej pętli do punktu.

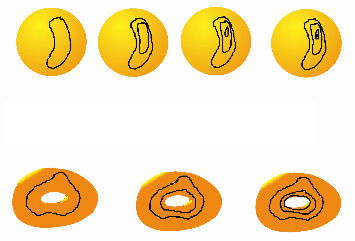
Co jednak z wyżejwymiarowymi uogólnieniami? Czy hipersfera - trójwymiarowa sfera w czterowymiarowej przestrzeni też jest jedynym rodzajem obiektów (rozmaitością), która zachowuje się w taki sposób, czy też może istnieją jeszcze inne klasy trójwymiarowych i zwartych rozmaitości, które są jednospójne? A co z jeszcze wyższymi wymiarami?

Oryginalna hipoteza Poincarégo opierała się matematykom przez sto lat, w czasie których opublikowano wiele nieprawidłowych dowodów. Z uogólnioną jej wersją poszło lepiej: w 1961 roku udowodniono jej prawdziwość dla liczby wymiarów sfery równej 5 (E. C. Zeeman) i większej niż 6 (S. Smale). Rok później J. Stallings pokazał, że jest prawdziwa również dla 6 wymiarów, zaś dwadzieścia lat później M. Freedman zrobił to samo dla czterowymiarowych sfer. Wciąż jednak nie wiadomo było, jak udowodnić prawdziwość hipotezy Poincarégo dla 3-sfer.

W 2000 roku Clay Mathematics Institute z Massachusetts włączyło hipotezę Poincaré na listę siedmiu najważniejszych nierozwiązanych problemów matematycznych - za rozwiązanie każdego z nich można otrzymać 1 mln dolarów. Pierwszy pretendent do nagrody pojawił się już dwa lata później, niestety jego (zaledwie pięciostronicowy) dowód okazał się być błędny. Jednak już w ciągu roku w archiwum e-printów arXiv zostały zamieszczone trzy publikacje Rosjanina Grigorija Perelmana, który szybko ściągnął na siebie uwagę kolegów i mediów. Jego dowód hipotezy Poincarégo (a raczej jego uogólnienia - hipotezy Thurstona) nie zawierał żadnych widocznych pomyłek, i szybko w środowisku matematyków zapanowało przekonanie, że tym razem się udało. Okazało się jednak, że Perelman nie był zainteresowany wykonaniem kolejnego formalnego kroku ku uznaniu, sławie i pieniądzom, czyli opublikowaniem recenzowanej pracy w którymś z prestiżowych periodyków matematycznych (co było również warunkiem sine qua non dla otrzymania nagrody). Dowód był napisany wyjątkowo trudnym językiem, a w wielu (oczywistych dla autora) miejscach został zaledwie naszkicowany: w sumie artykuły Perelmana liczyły sobie niespełna 70 stron. Opis dowodu Perelmana, napisany przez B. Kleinera i J. Lotta, to już 192 strony, zaś jeszcze większa praca przeprowadzająca przez dowód krok po kroku została opublikowana miesiąc temu przez J. Morgana i G. Tiana. Do wyścigu dołączyli też chińscy matematycy Huai-Dong Cao i Xi-Ping Zhu, których "Kompletny dowód twierdzenia Poincarego i geometryzacji" (328 stron!) ukazał się ostatnio w Asian Journal of Mathematics. W tym ostatnim przypadku autorzy zresztą nie kryli, że chcą zapisać dowód twierdzenia na swoje konto.

Gdyby Perelman dostał medal Fieldsa - a takie plotki potwierdzane są pośrednio również przez organizatorów - byłoby to jednoznacznym sygnałem, że to jemu należy się cześć i chwała za rozwiązanie matematycznej zagadki stulecia.